نویسنده: Vitale Sparacello
مقدمه ای آرام بر یادگیری عمیق هندسی
آشنایی بیشتر با یادگیری عمیق هندسی
مقدمه
هوش مصنوعی دنیای ما را تغییر داده است و سیستم های هوشمند بخشی از زندگی روزمره ما هستند و صنایع را در همه بخش ها کنترل می کنند.در میان تمام رشته های هوش مصنوعی، یادگیری عمیق در حال حاضر داغ ترین موضوع است و متخصصان یادگیری ماشین با موفقیت شبکههای عصبی عمیق (DNN) را برای حل مشکلات چالش برانگیز در بسیاری از زمینههای علمی پیادهسازی کرده اند.
امروزه، ماشینها میتوانند ببینند که یک چهارراه چقدر شلوغ است، میتوان با فیلسوفان خیالی گفتگوهای دلپذیری داشت، یا میتوانیم به سادگی از تماشای هوش مصنوعی که گیمرهای حرفهای مورد علاقه ما را نابود میکنند، لذت ببریم. اما، تا زمانی که داده های کافی برای آموزش مدل ها نداشته باشیم، تنها این مباحث محدود به تخیل آدمی است.
بهطور کلی، دادههایی که برای آموزش مدلهای یادگیری عمیق استفاده میکنیم به دو حوزه اصلی تعلق دارند:
داده های اقلیدسی: داده هایی که در فضاهای خطی چند بعدی نشان داده می شوند، از فرضیه های اقلیدسی تبعیت می کنند. به عنوان مثال، داده های متنی یا جدولی (مثلاً قیمت Dogecoin در طول زمان) هستند.
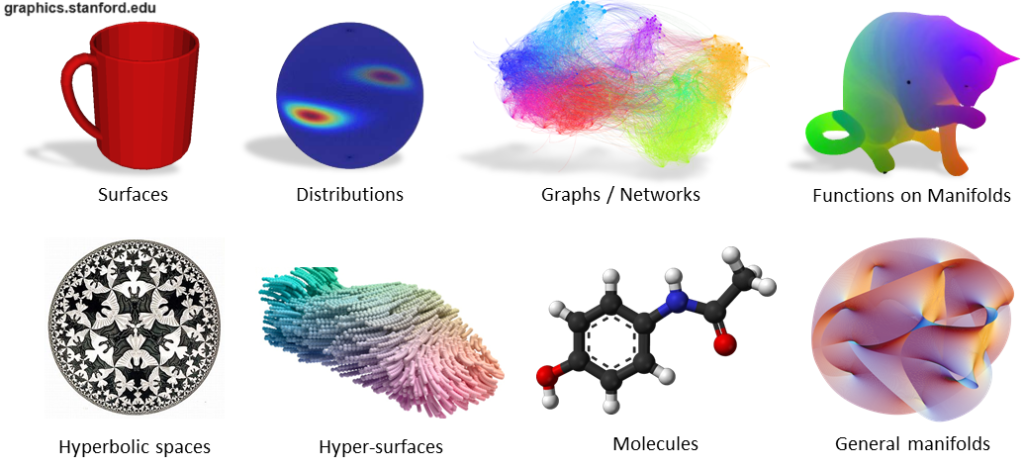
دادههای غیراقلیدسی: در اصطلاح گستردهتر، دادههایی که از فرضیههای اقلیدسی تبعیت نمیکنند (مثلاً در این حوزهها فاصله بین دو نقطه یک خط مستقیم نیست). به عنوان مثال می توان به ساختارهای مولکولی، تعاملات شبکه های اجتماعی یا سطوح سه بعدی مشبک اشاره کرد.
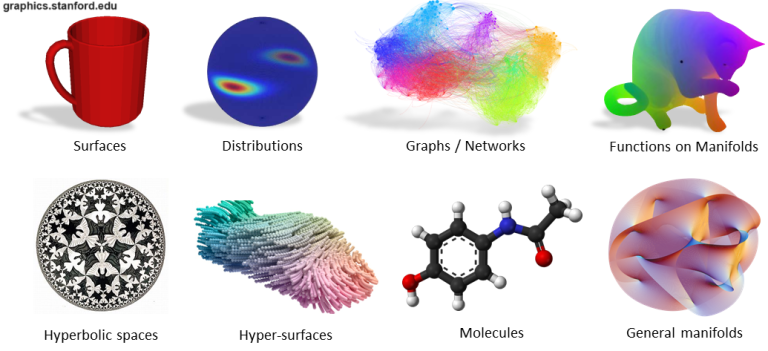
نمونه هایی از داده های غیر اقلیدوسی
در هوش مصنوعی کاربردی، مدلهای یادگیری عمیق با دادههای اقلیدسی بسیار خوب کار میکنند، اما هنگام برخورد با دادههای غیراقلیدسی مشکل دارند. این یک مشکل بزرگ است زیرا یافتن داده هایی از این نوع در همه زمینه های علمی رایج است!
خوشبختانه، در چند سال گذشته، پزشکان ML (❤️ ) اصطلاح Geometric Deep Learning را ابداع کردند و شروع به رسمی کردن نظریه برای حل این مشکل کردند. این میدان هوش مصنوعی در حال ظهور سعی میکند DNNها را برای مقابله با حوزههای غیراقلیدسی با استفاده از اصول هندسی تعمیم دهد.
چرا هندسه اینقدر مهم است؟
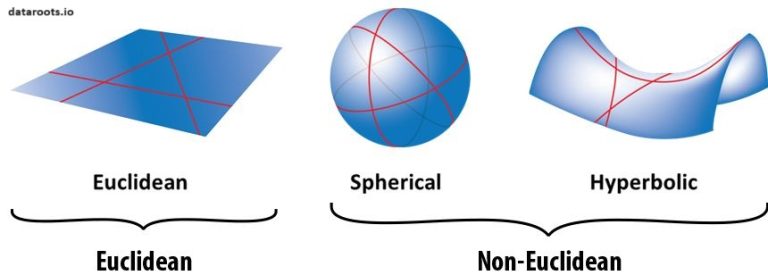
از زمان یونانیان، هندسه اقلیدسی تنها رشته ای برای مطالعه ویژگی های هندسی بوده است. حتی در حال حاضر، هندسه اقلیدسی ابزاری قدرتمند برای توصیف بسیاری از پدیده های اطراف ما است. همانطور که قبلا دیدیم، از اصول ساده پیروی می کند و درک آن ساده است: به عنوان مثال. فاصله بین 2 نقطه یک خط مستقیم است یا تمام زوایای قائم با هم متجانس هستند.
با این حال، در طول قرن نوزدهم، بسیاری از ریاضیدانان هندسه های جایگزین را با تغییر فرضیات اقلیدس به دست آوردند. آنها همچنین متوجه شدند که این هندسه های جدید در توضیح نحوه تعامل اجسام در فضاهای مختلف بسیار خوب هستند. به عنوان مثال می توان به هندسه هذلولی لوباچفسکی یا هندسه بیضوی ریمان اشاره کرد.
متأسفانه، همه این هندسه های مختلف در چندین زمینه مستقل از هم جدا شدند. یک سوال قانونی در آن زمان این بود: کدام یک حقیقی است؟
خوشبختانه در سال 1872، پروفسور فلیکس کلین این معمای پیچیده را با کار خود به نام برنامه ارلانگن حل کرد. او چارچوبی را برای یکسان سازی تمام هندسه ها با استفاده از مفاهیم عدم تغییر و تقارن پیشنهاد کرد.

پروفسور فلیکس کلاین و کارهایش (منبع تصویر)
این ایده منجر به طرحی برای تعریف هندسه شد که فقط با کمک دامنه ای که داده ها در آن زندگی می کنند و چه تقارنی هایی باید رعایت کنند مشخص می شود.
برنامه ارلانگن تأثیر قابل توجهی در تمام زمینه های علمی، به ویژه در فیزیک، شیمی و ریاضی داشت.
یادگیری عمیق در مورد داده های غیر اقلیدسی
محققان یادگیری عمیق استثنایی هستند. هر روز بیش از 100 مقاله ML در Arxiv منتشر می شود! ما مملو از مدلهای جدیدی هستیم که نوید حل مشکلات را بهتر از سایرین میدهند، اما قوانین یکسانی برای تعریف معماریهای هوش مصنوعی نداریم که بتوانند ویژگیهای خود را در همه حوزههای داده ممکن تعمیم دهند.
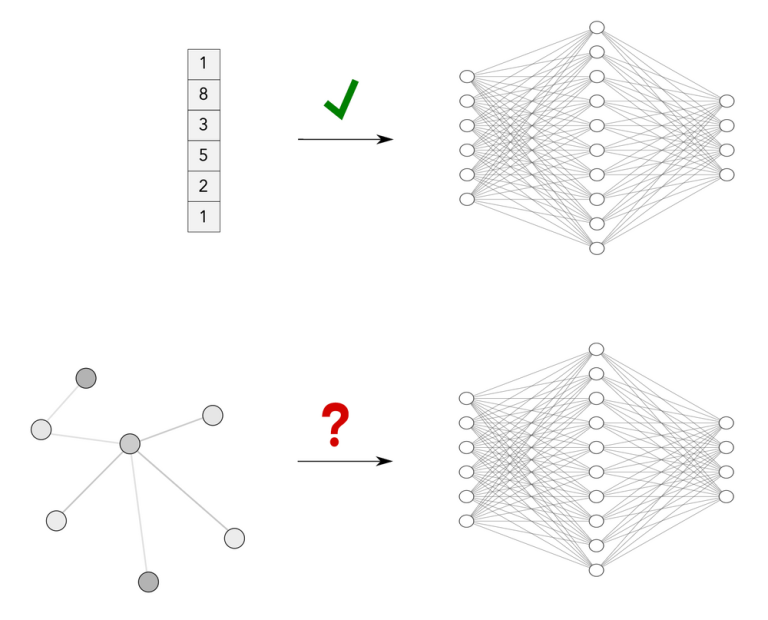
DNN ها معمولاً با ورودی های ساختار یافته با اندازه ثابت مانند بردارها کار می کنند. همه چیز با داده های غیر اقلیدسی پیچیده می شود.(منبع)
شبکه های عصبی کانولوشنال (CNN) یکی از مهم ترین الگوریتم ها در یادگیری ماشین هستند. CNN ها می توانند اطلاعات سطح بالایی را از تصاویر، فیلم ها یا سایر ورودی های بصری به دست آورند. به همین دلیل آنها به طور گسترده ای برای حل مشکلات بینایی کامپیوتر استفاده شده اند.
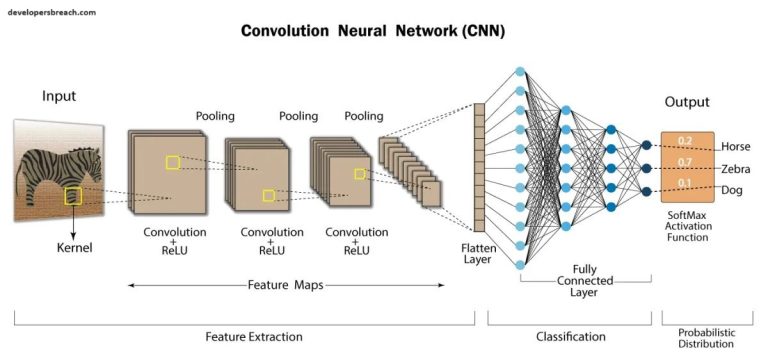
CNN ها شبکه های عصبی خاصی هستند که قادر به استخراج اطلاعات از ورودی های بصری با استفاده از Convolution می باشند. (منبع)
اصطلاح Convolution به یک عملیات بسیار ساده اشاره دارد: یک ماتریس کوچک (معمولاً فیلتر نامیده میشود) را روی یک تصویر بکشید و یک ضرب بر حسب عنصر و به دنبال آن یک مجموع برای تولید ماتریس دیگری انجام دهید (به gif زیر مراجعه کنید). با این عملیات امکان استخراج ویژگی های سطح پایین از تصویر ورودی مانند لبه ها، اشکال یا نقاط روشن وجود دارد.
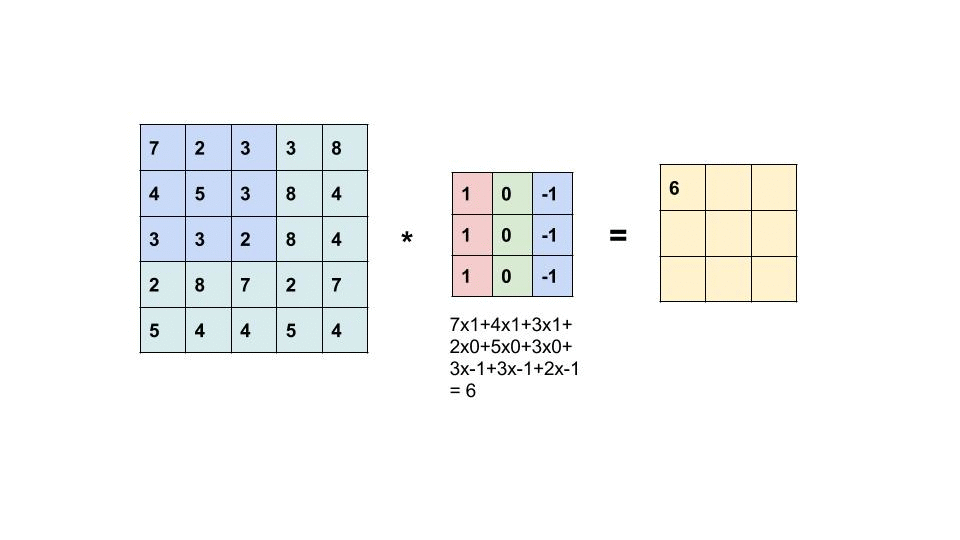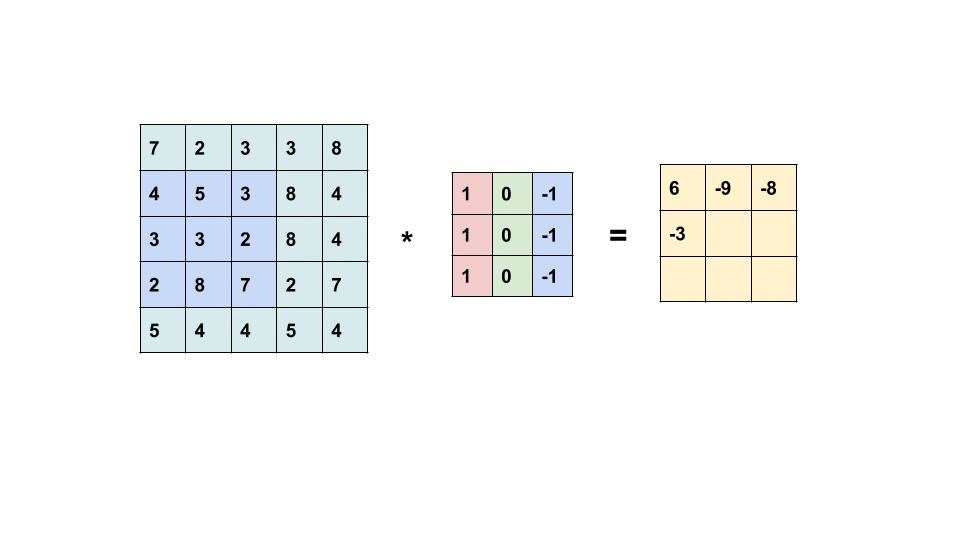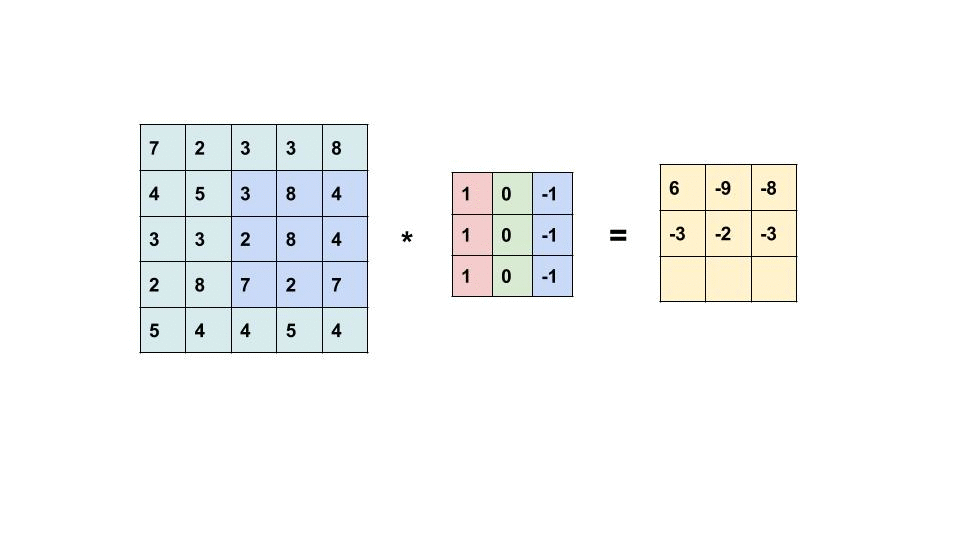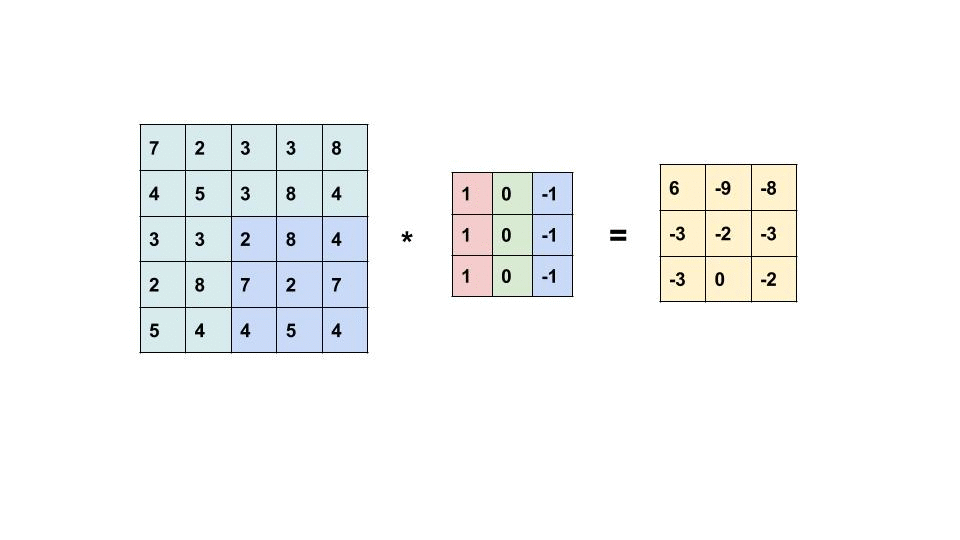
یک مثال از Convolution (منبع)
Journal Reference
- Yuta Kanaya, Nobuyuki Kawai. Anger is eliminated with the disposal of a paper written because of provocation. Scientific Reports, 2024; 14 (1) DOI: 10.1038/s41598-024-57916-z
- https://www.sciencedaily.com/releases/2024/04/240409123905.htm
کانولوشن ها کار می کنند زیرا ما تصاویر را با استفاده از یک ساختار داده دو بعدی نمایش می دهیم. به این ترتیب می توان وزن های شبکه را با استفاده از فیلترهای کانولوشن به اشتراک گذاشت و اطلاعات را بدون توجه به جابجایی یا اعوجاج تصاویر ورودی استخراج کرد (همان فیلتر در تمام تصویر اعمال می شود). این اولین نمونه از ساده سازی مسئله با استفاده از هندسه داده های ورودی بوده است.
چگونه می توانیم این ایده را برای حوزه های دیگر رسمی و گسترش دهیم؟ شاید استفاده از اصول هندسی بتواند مانند گذشته به ما کمک کند.
چرا یادگیری بر روی داده های غیر اقلیدسی پیچیده است؟
متأسفانه، داده های غیر اقلیدسی از نفرین ابعادی رنج می برند! برای توضیح بهتر، اجازه دهید یکی از اصلی ترین کاربردهای ML را در نظر بگیریم: یادگیری نظارتی. هدف اصلی آن یادگیری حل یک کار با تقریب یک تابع با استفاده از داده های آموزشی است. (توابع حاصل آموزش DNN ها هستند، در قسمت زیر از کلمه تابع استفاده می کنیم)
به لطف قضیه تقریب جهانی، می دانیم که می توانیم حتی از یک شبکه عصبی ساده برای بازتولید هر تابع پیوسته (با هر دقت دلخواه) استفاده کنیم.
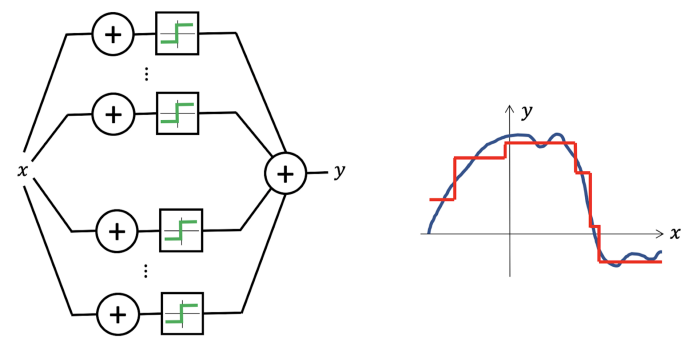
شبکههای عصبی تقریبکنندههای جهانی هستند: تنها با یک لایه پنهان، میتوانند ترکیبی از توابع مرحلهای را نشان دهند که امکان تقریب هر تابع پیوسته را با دقت دلخواه فراهم میکند. (منبع)
متأسفانه، همه چیز در ابعاد بالا پیچیده می شود: ما به تعداد نمایی نمونه نیاز داریم تا حتی ساده ترین تابع چند بعدی را تقریب کنیم.
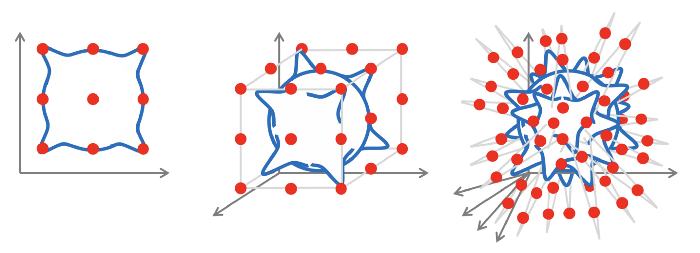
تقریب یک تابع پیوسته در ابعاد چندگانه. (منبع)
یک راه حل متداول برای این مشکل این است که داده های با ابعاد بالا را به فضایی با ابعاد کم بفرستید (به عنوان مثال کاهش ابعاد با استفاده از الگوریتم PCA) با این حال، این همیشه امکان پذیر نیست زیرا ممکن است اطلاعات مهم را نادیده بگیریم.
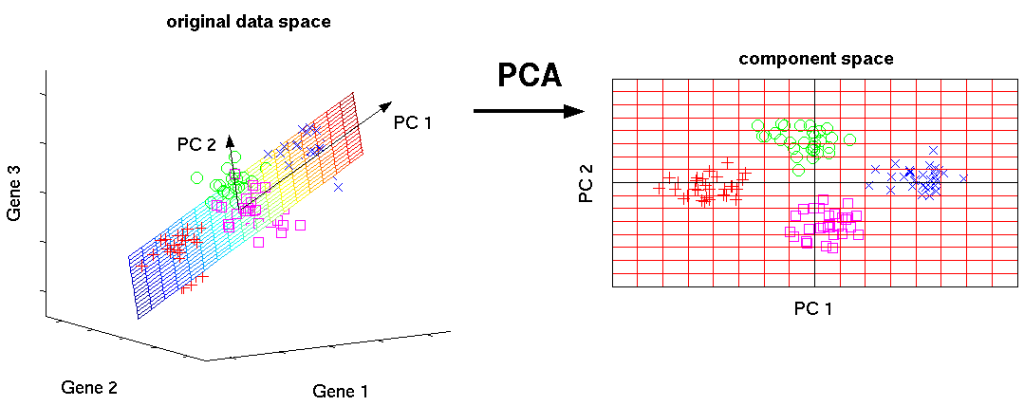
با PCA می توان ابعاد را کاهش داد، اما آیا همیشه همان چیزی است که ما می خواهیم؟ (منبع)
برای غلبه بر این مشکل می توانیم از ساختار هندسی داده های ورودی استفاده کنیم. این ساختار به طور رسمی Geometric prior نامیده می شود و برای رسمی کردن نحوه پردازش داده های ورودی مفید است.
به عنوان مثال، در نظر گرفتن یک تصویر به عنوان یک ساختار 2 بعدی به جای اینکه یک بردار d-بعدی از پیکسل ها یک پیشین هندسی است. اولویتها مهم هستند زیرا با استفاده از آنها، میتوان تعداد توابعی را که میتوانیم با دادههای ورودی تطبیق دهیم محدود کرد و مشکل با ابعاد بالا را قابل حل کرد.
به عنوان مثال با در نظر گرفتن مقدمات هندسی، می توان توابعی را شناسایی کرد که:
می تواند تصاویر را مستقل از هر تغییر (CNN) پردازش کند.
می تواند داده های پیش بینی شده روی کره ها را مستقل از چرخش ها پردازش کند (CNNs کروی).
می تواند داده های گراف را مستقل از ایزومورفیسم (شبکه های عصبی گراف) پردازش کند.
یادگیری عمیق هندسی دو اولویت اصلی را شناسایی می کند که توابع ما باید برای ساده کردن مسئله و تزریق مفروضات هندسی به داده های ورودی رعایت کنند:
تقارن: توسط توابعی که یک شی را ثابت میگذارند رعایت میشود، آنها باید ترکیبپذیر، معکوس باشند و باید حاوی هویت باشند.
جداسازی مقیاس: تابع باید تحت تغییر شکل جزئی دامنه پایدار باشد.
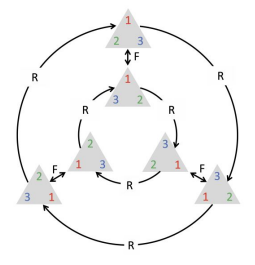
چرخش تابعی است که به تقارن در حوزه مثلث متساوی الاضلاع احترام می گذارد. (منبع)